Normal(mu, sigma)
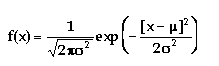
mu = shift parameter = mean
sigma = scale parameter = standard deviation
The Normal distribution is a unbounded continuous distribution. It sometimes called a Gaussian distribution or the bell curve. Because of its property of representing an increasing sum of small, independent errors, the Normal distribution finds many, many uses in statistics. It is wrongly used in many situations. Possibly, the most important test in the fitting of analytical distributions is the elimination of the Normal distribution as a possible candidate. (see Johnson et. al.1)
The Normal distribution is used as an approximation for the Binomial distribution when the values of n,p are in the appropriate range. The Normal distribution is frequently used to represent symmetrical data, but suffers from being unbounded in both directions. If the data is known to have a lower bound, it may be better represented by suitable parametrization of the Lognormal, Weibull, or Gamma distributions. If the data is known to have both upper and lower bounds, the Beta distribution can be used, although much work has been done on truncated Normal distributions
